Rovina

SVĚT GEOMETRIE

Normálový vektor, obecný tvar rovnice

Normálový vektor n = (A, B, C)

Nerovnoběžné vektory ležící v rovině s₁ = (a₁,b₁,g₁) a s₂ = (a₂,b₂,g₂

Obecný tvar rovnice: Ax + By + Cz + D = 0

1. Po a vektor n :

A (x - x₀) + B (y - y₀) + C (z - z₀) = 0

2. Po a s₁ a s₂

a)  n = s₁ x s₂  a (1)

b) Parametrický tvar :

3. Třemi body (neležícími na přímce) Po, P₁, P₂. Určit n = Po P₁ x Po P₂ a (1)

4. Průsečíky s osami souřadnic (úsekový tvar):

Příklad:

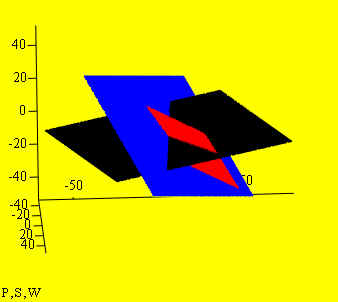
Po = [2, 4, -1], p₁ = (2, 3, -1), p₂ = (1, -1, 2)

Po = [2, 4, -1], s₁ = (1, -2, 4), s₂ = (-3, 3, -1)

Po = [2, 4, -1], w₁ = (-3, -5, -2), w₂ = (2, 2, -1)

průsečnice ve stejném bodě Po